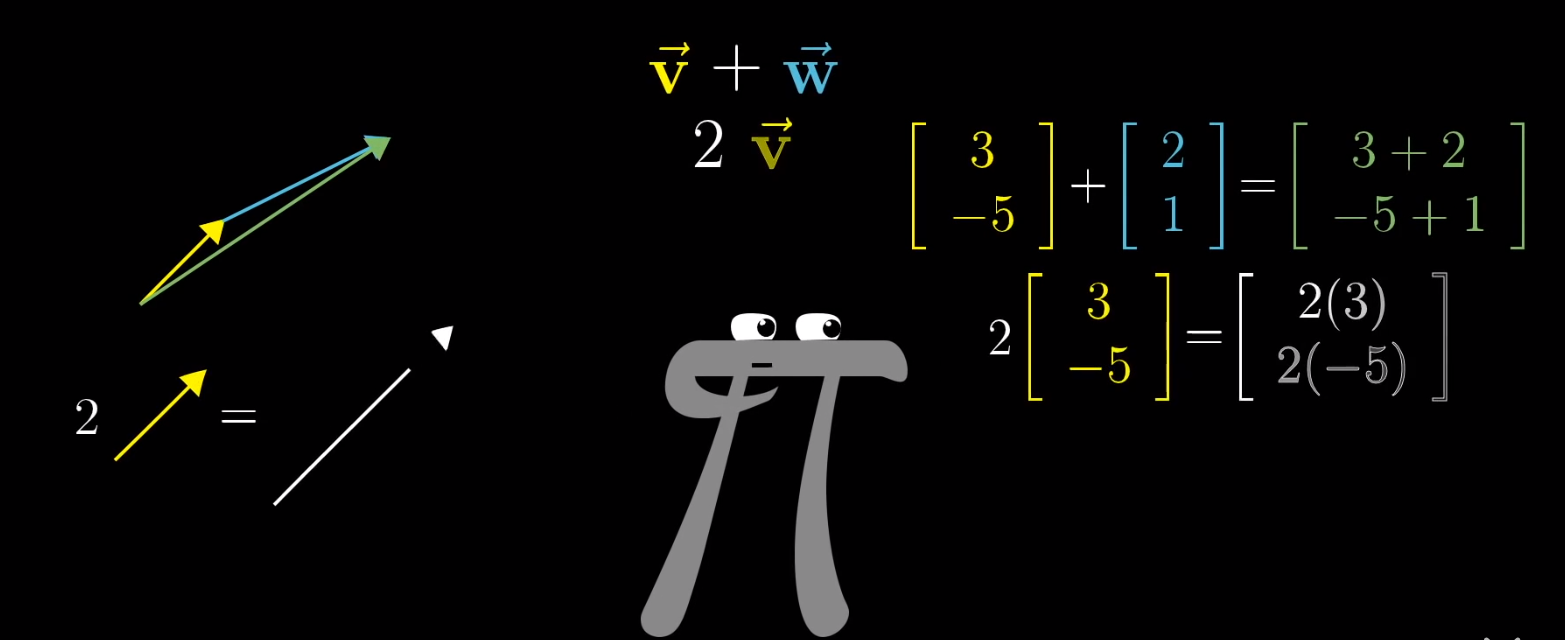一般来讲,有以下三种看待向量的观点,分别是物理专业视角、计算机专业视角以及数学专业视角下的向量,三者看似不同却有所关联。
物理专业视角
从物理视角看,向量是空间中的箭头,决定一个向量的是它的长度和方向,只要这2个特征相同,就可以自由移动一个向量而保持其不变。
即使这个向量移动到空间的任何位置,只要这个向量的长度和方向未发生变化,则这个向量仍然没有发生任何变化。
计算机视角
从计算机视角看,向量是有序的数字列表。
例如:
数学专业视角
从数学视角看,向量可以是任何东西,只需要保证两个向量相加以及数字与向量相乘是有意义的。
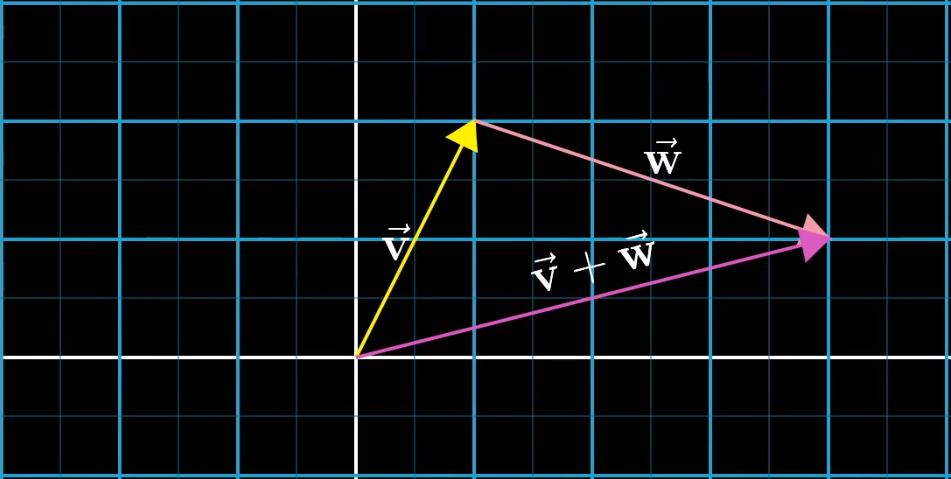
1、向量加法:
其定义如下:
其计算方式如下:
2、向量数乘:
其定义如下:
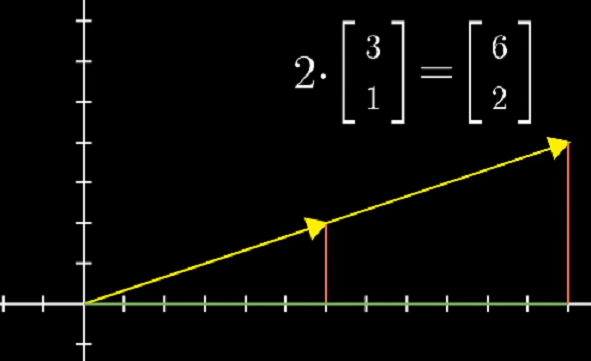
其计算方式如下:
向量加法和向量数乘贯穿线性代数始终,二者起着重要的作用。
小结
向量可以理解为空间中的箭头,也可以理解为有序的数字列表,线性代数的能力很少体现在其中任意一个单独的观点上,而是体现在线性代数可以在二者之间相互转化。因此,我们在理解线性代数的时候,可以从线性代数的几何直观和数字计算2个层面去理解。